Linearität (Physik)

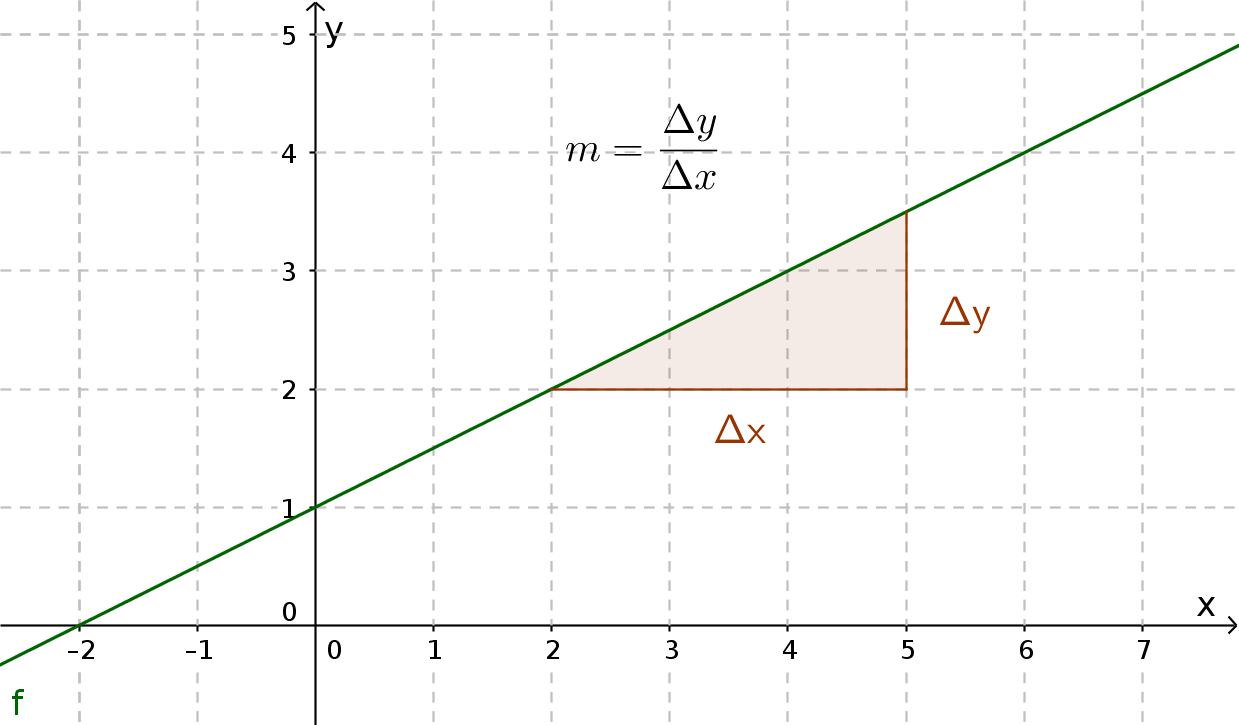
Von Linearität in Physik, Chemie und Technik wird gesprochen, wenn ein Zusammenhang zwischen zwei physikalischen Größen durch eine lineare Funktion dargestellt werden kann.

Grundlage

Eignen sich zur Beschreibung des Verhaltens eines Bauelementes (eines Gerätes, einer Einrichtung) oder eines physikalischen Zusammenhangs eine Eingangsgröße ${\displaystyle x}$ und eine Ausgangsgröße ${\displaystyle y}$, und genügen diese Größen der Gleichung

${\displaystyle y=m\cdot x b\quad {\text{mit }}\ m,b={\text{reelle Konstanten,}}}$

so spricht man von einem linearen Bauelement oder einer linearen Funktion (genauer: affin-lineare Funktion). In einem rechtwinkligen Koordinatensystem mit gleichmäßig geteilten Achsen wird der Zusammenhang zwischen dem Ausgangssignal und dem Eingangssignal durch eine gerade Kennlinie dargestellt.

Im Sonderfall ${\displaystyle b=0}$ ist der Zusammenhang durch Proportionalität geprägt. Bei proportionalem Zusammenhang geht die Kennlinie durch den Koordinatenursprung. Bei dieser Linearität im engeren Sinne, d. h. unter Erfüllung der Linearitätsbedingungen im Sinne der linearen Algebra, gilt zusätzlich

${\displaystyle {\frac {y}{x}}=m={\text{konst .}}}$

Gleichbedeutend gilt als Kennzeichen einer linearen Kennlinie, wenn ihre Steigung konstant ist,

${\displaystyle {\frac {\Delta y}{\Delta x}}=m={\text{konst ,}}}$

und zwar unabhängig von der Größe von ${\displaystyle \Delta x}$ und von der Lage des Arbeitspunktes, ab dem sowohl ${\displaystyle \Delta x}$ als auch ${\displaystyle \Delta y}$ zählen. Bei einer stetig gekrümmten Kennlinie kann eine lineare Näherung im Rahmen eines Kleinsignalverhaltens verwendet werden, soweit bei kleinen Werten von ${\displaystyle |\Delta x|}$ die Abweichung der Kurve von ihrer Tangente (im jeweils gewählten Arbeitspunkt) noch gering ist.

Wird beispielsweise das Volumen ${\displaystyle V}$ einer Flüssigkeitsmenge in Abhängigkeit von der Celsiustemperatur ${\displaystyle t}$ beschrieben durch ${\displaystyle V=V_{0}(1 \alpha t \beta t^{2} \gamma t^{3} \cdots )}$, und bringen dabei die Summanden mit ${\displaystyle \beta ,\ \gamma ,\,\cdots \ }$ keinen beachtenswerten Beitrag, wohl aber der Summand ${\displaystyle \alpha t}$, so liegt eine Linearität der thermischen Ausdehnung vor.

In der Messtechnik

• Häufig liegt zwischen einer Messgröße (z. B. Konzentration eines Stoffes in der analytischen Chemie) und dem Messsignal (z. B. die elektrische Spannung eines Sensors) eine lineare Funktion zu Grunde. Angestrebt wird bei einem Messgerät möglichst Proportionalität. Dazu wird im Rahmen der Signalbearbeitung in einer Messkette nicht nur das Signal verstärkt, sondern bei Bedarf zusätzlich der Nullpunkt verschoben. Im Fall des nebenstehend gezeigten Messgerätes ist eine Möglichkeit vorhanden, den Zeiger von außen zu verdrehen und damit den Nullpunkt einzustellen.

• In nebenstehendem Bild besteht im zur oberen Skale gehörenden Messbereich ein nichtlinearer Zusammenhang zwischen der Messgröße und dem Ausschlag bzw. dem Winkel des Zeigers. Durch eine ebenfalls nichtlineare Skalenteilung wird der ablesbare Wert dennoch proportional zur Messgröße.

In der Elektrotechnik

• Eine Spannungsquelle wird als lineare Spannungsquelle bezeichnet, wenn die Klemmenspannung ${\displaystyle U_{\text{kl}}}$ mit steigender Stromstärke ${\displaystyle I}$ abnimmt gemäß der Gleichung

${\displaystyle U_{\text{kl}}=U_{0}-I\,R_{\text{i}}}$.

• Die grundlegenden passiven Bauelemente ohmscher Widerstand, Spule und Kondensator werden in einem Wechselstromkreis als lineare Widerstände bezeichnet, da sie auf eine harmonische Schwingung ${\displaystyle \Delta x}$ der Eingangsgröße mit einer ebenfalls harmonischen Schwingung ${\displaystyle \Delta y}$ der Ausgangsgröße bei gleicher Frequenz reagieren. Dabei sind diese Größen die elektrische Spannung ${\displaystyle U}$ und elektrische Stromstärke ${\displaystyle I}$. – Halbleiterbauelemente verhalten sich in aller Regel nichtlinear.

• In der Kennlinie eines Feldeffekttransistors ist der Zusammenhang zwischen der Steuerspannung ${\displaystyle U_{\mathrm {GS} }}$ und der gesteuerten Stromstärke ${\displaystyle I_{\mathrm {D} }}$ eines Feldeffekttransistors dargestellt. Es lassen sich zwei Bereiche unterscheiden, wobei die Grenze fließend ist.
  • Im Bereich 0 … −1 V kann die Kurve in guter Näherung als geradlinig angesehen werden; es liegt Linearität vor. Hier folgt einer Spannungsänderung ${\displaystyle \Delta U_{\mathrm {GS} }}$, die ab einem Arbeitspunkt gezählt wird, eine proportionale Änderung der Stromstärke ${\displaystyle \Delta I_{\mathrm {D} }}$. Bei einer sinusförmigen zeitlichen Änderung von ${\displaystyle \Delta U_{\mathrm {GS} }}$ folgt ${\displaystyle \Delta I_{\mathrm {D} }}$ ebenfalls sinusförmig.
  • Im Bereich −1 … −3 V ist die Funktion nichtlinear. Hieraus resultieren Verzerrungen: Bei sinusförmigem zeitlichem Verlauf von ${\displaystyle \Delta U_{\mathrm {GS} }}$ folgt ${\displaystyle \Delta I_{\mathrm {D} }}$ mit einem nicht sinusförmigen Verlauf.

In der Mechanik

Entsprechend der lateinischen Bedeutung des Wortes linea erfolgt u. a. eine Unterscheidung der Bewegungsrichtung von Körpern danach, ob die Bewegung entlang einer entsprechend ausgeprägten geraden Linie erfolgt (linear) oder nicht (nicht linear). Beispiel: In einem Verbrennungsmotor führt der Hubkolben eine geradlinige Bewegung aus (eine ungleichmäßige Translation) und die mit ihm verbundene Kurbelwelle eine kreisförmige Bewegung (im stationären Zustand eine gleichmäßige Rotation).

In der Chemie

Zur Klassifikation der Molekülgeometrie kann ein Molekül linear oder gewinkelt bezeichnet werden. Bei linearen Molekülen beträgt der Bindungswinkel 180°.

Soweit bei chemischen Analysen elektrische oder andere physikalische Größen gemessen werden, sind Zusammenhänge bekannt, die durch lineare Funktionen beschrieben werden; dazu drei Beispiele:

• In wässerigen Lösungen ist der Zusammenhang zwischen Konzentration und elektrolytischer Leitfähigkeit meistens ein proportionaler.
• Der Zusammenhang zwischen pH-Wert und elektrischer Spannung ist bei geeigneten Elektroden „linear“, siehe Bild.
• Wird die Temperaturabhängigkeit einer Reaktionsgeschwindigkeit in einem Arrheniusgraphen aufgetragen, erhält man bei kinetisch einfachen Reaktionen einen „linearen Zusammenhang“. Aus der Steigung des „linearen Graphen“ erhält man die Aktivierungsenergie.

Bei der Methodenvalidierung, wie sie z. B. in der analytischen Chemie oder Forensik verwendet wird, ist ein statistischer Test auf Linearität nach Mandel, der sogenannte Mandel-Test (oder Mandel-Anpassungstest) üblich, anhand dessen bestimmt wird, welches Regressionsmodell (lineare oder quadratische Regression) für den vorliegenden Untersuchungsfall anzunehmen ist.

Weblinks

Einzelnachweise